Have you got a tomographic volume reconstruction of a porous sample and want to quantify the porosity? Interested in the statistical analysis of the pore distribution of your sample? Let’s look at some quantitative ways to characterise the properties of your sample with Python.
We start from the volume data of our porous sample and we segment it, so to produce a binary volume where the pores will be labelled as ‘1’ and the rest will be labelled as ‘0’.
There are many ways to segment your data using thresholding or other methods. You can read few excellent examples here or here.
OK, here’s my example of the virtual slice of a porous material and the corresponding segmented slice. Note that we are going to work on a single slice (2D array), but the method can easily be extended to a 3D array.
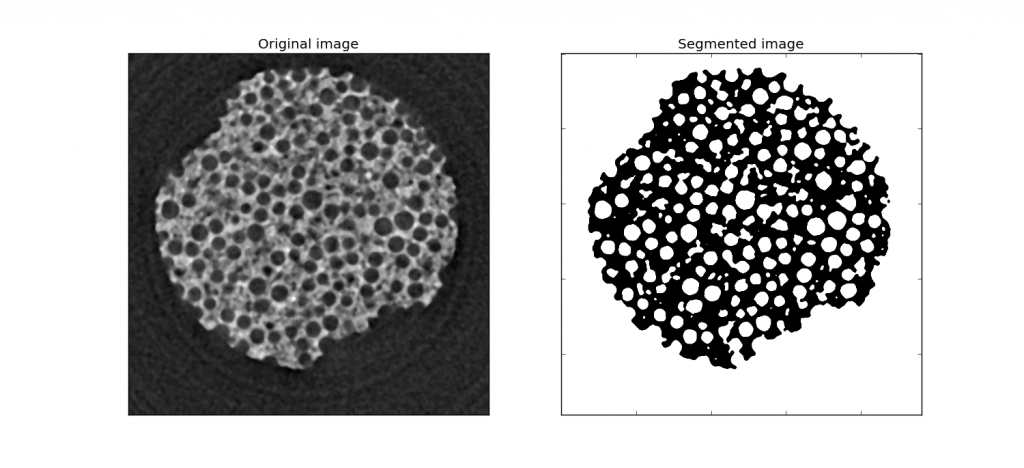
We are going to use the scikit-image module to:
The first bit is straightforward and is done in this way.
from skimage.external import tifffile as tif
import numpy as np
from skimage.filters import threshold_otsu
from scipy import ndimage
# Read the image
raw = tif.imread('image.tif')
# Normalize to 1
raw *= (1.0/raw.max())
# Calculate otsu threshold
otsu = threshold_otsu(raw)
# Segment the pores
segm = fil < otsu
# Generate the structuring element for the morphological operation that follows
s = ndimage.morphology.generate_binary_structure(2,2)
# Label the pores
labelled_image, n_labels = ndimage.label(segm, structure=s)A short note on the last two lines. The structuring element ‘s’ will define what features we want to consider as ‘connected’. With our choice we assume that white pixels that touches along the edges or the corners are connected. We could choose to exclude the corners using
s = ndimage.morphology.generate_binary_structure(2,1)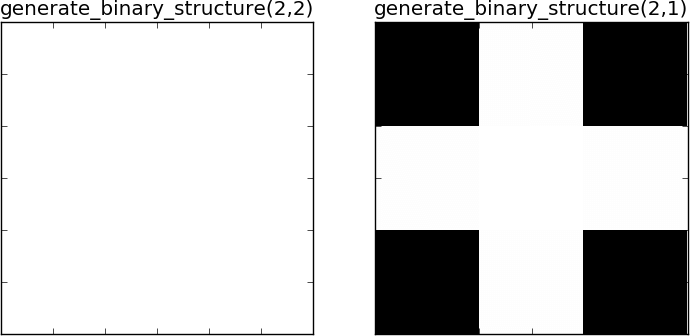
The ndimage.label command returns an array with the same size as the input, where each unique feature (that is each connected region of white pixels) is assigned a unique label.
The second output of the command is the number of features that are found in the image.
Take a look at the result in the figure below. The labelled image is on the left hand side. On the right side, it is the labelled image overlapped with the original image.

OK done. Now let’s plot the histogram, that is the number of pores in each volume range.
# Compute the size of each region:
sizes = ndimage.sum(segm, labelled_image, range(n_labels + 1))[2:]
# Set the range, excluding pixels of size 1
rg = (2, sizes.max())
#Set the number of bins
nbins = int(sizes.max()-2)
# Calculate the histogram
hh, bin_edges = np.histogram(sizes, range = rg, bins = nbins)
# set the abscissa in the middle of the bin
pix = 0.025 # Pixel size, mm
x = 0.5*(bin_edges[:-1] + bin_edges[1:])*px**2
# bar width in the histogram bar plot
width=x[2]-x[1]
# Bar plot
with plt.style.context(('bmh')):
plt.bar(x,hh, width, color='r')
plt.xlabel('Pore size (mm$^{2}$)')
plt.ylabel('# pores')
plt.show()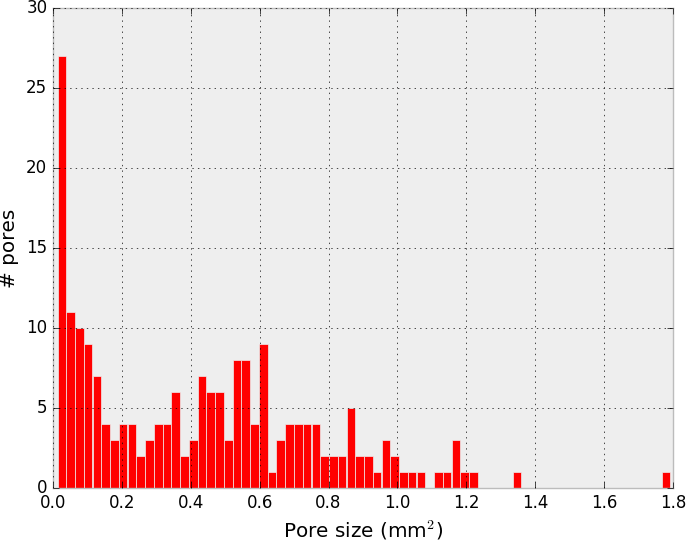
Done! Here is the quantitative analysis of the pore size distribution within the slice.
| Cookie | Duration | Description |
|---|---|---|
| cookielawinfo-checkbox-analytics | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Analytics". |
| cookielawinfo-checkbox-functional | 11 months | The cookie is set by GDPR cookie consent to record the user consent for the cookies in the category "Functional". |
| cookielawinfo-checkbox-necessary | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookies is used to store the user consent for the cookies in the category "Necessary". |
| cookielawinfo-checkbox-others | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Other. |
| cookielawinfo-checkbox-performance | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Performance". |
| viewed_cookie_policy | 11 months | The cookie is set by the GDPR Cookie Consent plugin and is used to store whether or not user has consented to the use of cookies. It does not store any personal data. |