Hi everyone! In this post we are going to work through an example to create quick visualisations of 3D network graphs with Python and the mplot3d toolkit of the Matplotlib.
Analysing the structure of complex networks is a fascinating problem, involving rich mathematics and data science skills. Mathematical tools of graph theory enable studying complex relational networks without necessarily resorting to visual intuition, and that’s great for abstraction to complicated, multi-dimensional networks. Humans however are visual animals (30% of our brains is dedicated to vision), and visualising information help us understanding.
At Instruments & Data Tools we develop methods to study complex structural networks in biological structures like roots or neurons. This kind of structures can be measured using, for instance, Computed Tomography (CT) or Optical Projection Tomography. Unlike more general networks (for example social media networks) that can have any number of dimensions depending on the parameters, biological networks are inherently 3D in structure. That means that understanding the 3D structure is often the key to understanding the function. That is why a lot of work is being done around the world to develop 3D imaging methods.
We decided to use NetworkX for our work. The reason are that NetworkX is extremely versatile, very well documented, and widely used by the community. The example we’ll show here starts from a synthetic random network generated with Networkx.
Now, NetworkX has not been designed with the primary intent of drawing graphs. Its main strength is quantitative analysis of graphs. NetworkX supports exporting graphs into formats that can be handled by graph plotting tools such as Cytoscape, Gephior, Graphviz, and also Plotly (If you are interested in Plotly, check out our posts on interactive scatter plots and choropleth maps). On top of that, 2D graph drawing is possible using Matplotlib.
The spirit of this example is to show an easy way to leverage the mplot3d toolkit to produce quick 3D network visualisations within the same script used to analyse the network. It is not meant to replace beautiful professional visualisations (such as things you can create with the packages linked above), rather to provide a simple way to start understanding your data.
Alright, let’s get started. Here’s the list of imports.
import networkx as nx
import random
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as npThe core of our script is made of two functions. The first is used to generate a 3D random graph. The second function is used to produce a 3D plot of it.
Here’s the code. We’ll going to write it here and explain it below.
def generate_random_3Dgraph(n_nodes, radius, seed=None):
if seed is not None:
random.seed(seed)
# Generate a dict of positions
pos = {i: (random.uniform(0, 1), random.uniform(0, 1), random.uniform(0, 1)) for i in range(n_nodes)}
# Create random 3D network
G = nx.random_geometric_graph(n_nodes, radius, pos=pos)
return GThe first line is used to recursively generating a 3D random network as a dict of points. The output of that is something that looks like this:
{0: (0.13436424411240122, 0.8474337369372327, 0.763774618976614),
1: (0.2550690257394217, 0.49543508709194095, 0.4494910647887381)
…
}The second line is used to create a random geometric graph. The inputs are the number of nodes in the network, the radius value and, obviously, the position of the nodes. The parameters radius is used to specify if two nodes are connected or not. Two nodes are connected by an edge if their distance is at most equal to radius. This will give the number of edges, that is the connections between the nodes.
One of the advantage of making a graphical visualisation of the 3D network, is that we can visually rank the nodes based on the number of their connections. In our example we will use two features: size and colour. Here’s the code
def network_plot_3D(G, angle, save=False):
# Get node positions
pos = nx.get_node_attributes(G, 'pos')
# Get number of nodes
n = G.number_of_nodes()
# Get the maximum number of edges adjacent to a single node
edge_max = max([G.degree(i) for i in range(n)])
# Define color range proportional to number of edges adjacent to a single node
colors = [plt.cm.plasma(G.degree(i)/edge_max) for i in range(n)]
# 3D network plot
with plt.style.context(('ggplot')):
fig = plt.figure(figsize=(10,7))
ax = Axes3D(fig)
# Loop on the pos dictionary to extract the x,y,z coordinates of each node
for key, value in pos.items():
xi = value[0]
yi = value[1]
zi = value[2]
# Scatter plot
ax.scatter(xi, yi, zi, c=colors[key], s=20+20*G.degree(key), edgecolors='k', alpha=0.7)
# Loop on the list of edges to get the x,y,z, coordinates of the connected nodes
# Those two points are the extrema of the line to be plotted
for i,j in enumerate(G.edges()):
x = np.array((pos[j[0]][0], pos[j[1]][0]))
y = np.array((pos[j[0]][1], pos[j[1]][1]))
z = np.array((pos[j[0]][2], pos[j[1]][2]))
# Plot the connecting lines
ax.plot(x, y, z, c='black', alpha=0.5)
# Set the initial view
ax.view_init(30, angle)
# Hide the axes
ax.set_axis_off()
if save is not False:
plt.savefig("C:\scratch\\data\"+str(angle).zfill(3)+".png")
plt.close('all')
else:
plt.show()
returnA couple of things to note here.
Note how to define the colour of the node: we get the value of the maximum number of edges in a single node, and use that value to define the colour scale to go from zero to such a maximum value.
At the same time we also use a simple linear scaling
s=20+20*G.degree(key)to scale the size of each node.
And here’s the code to create and visualise a random network with 200 nodes
n=200
G = generate_random_3Dgraph(n_nodes=n, radius=0.25, seed=1)
network_plot_3D(G,0, save=False)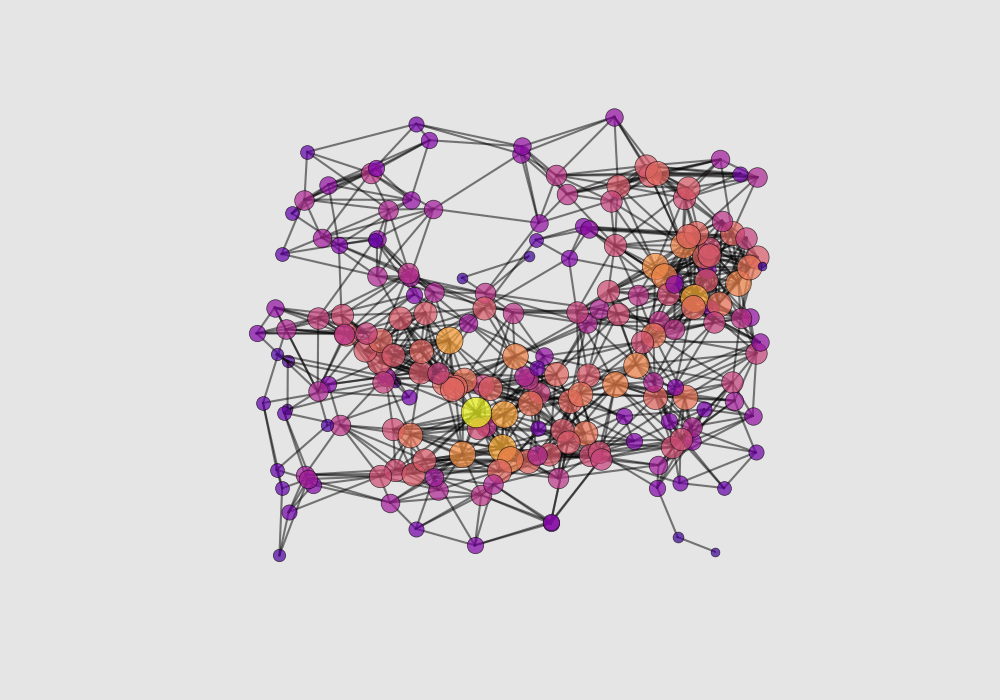
Finally, to make the video at the top of this page, we put these two functions in a loop, by recursively changing the number of nodes and the view angle. Note that we fix the random seed to reproduce exactly the same sequence of nodes each time.
for k in range(20,201,1):
G = generate_random_3Dgraph(n_nodes=k, radius=0.25, seed=1)
angle = (k-20)*360/(200-20)
network_plot_3D(G,angle, save=True)
print(angle)Well, that’s it for today. Thanks for reading!
| Cookie | Duration | Description |
|---|---|---|
| cookielawinfo-checkbox-analytics | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Analytics". |
| cookielawinfo-checkbox-functional | 11 months | The cookie is set by GDPR cookie consent to record the user consent for the cookies in the category "Functional". |
| cookielawinfo-checkbox-necessary | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookies is used to store the user consent for the cookies in the category "Necessary". |
| cookielawinfo-checkbox-others | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Other. |
| cookielawinfo-checkbox-performance | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Performance". |
| viewed_cookie_policy | 11 months | The cookie is set by the GDPR Cookie Consent plugin and is used to store whether or not user has consented to the use of cookies. It does not store any personal data. |